Project Background and motivation
Sequential Monte Carlo (SMC) methods are a general class of Monte Carlo procedures for sampling from sequences of probability distributions. Basic examples of these algorithms, termed particle filters, are frequently used in a variety of fields including signal processing, economics, and systems biology.
Recent methodological developments, one example being Particle MCMC and Particle Gibbs methods, have gained considerable popularity. However, they require algorithmic extensions and are particularly computationally expensive. Hence, software support for these procedures is currently in high demand.
This project aims at providing straightforward implementation of modern SMC/Particle MCMC methods by extending the C++ template class library of RcppSMC which is currently not supporting these methods.
Benefits for the R community are expected, firstly, as SMC practitioners who already use R can reduce execution time as well as time necessary for implementation in their everyday work. SMC developers, currently not using R as their first programming language of choice, hopefully see the benefits of this package and thus might consider using R more often in this domain in the future.
Summary of project results
RcppSMC did not allow a straightforward implementation of aforementioned algorithms prior to the GSoC 2021. This project aimed at providing support for modern SMC/MCMC hybrid procedures by extending RcppSMC.
Moreover, a separate R package, SVmodelRcppSMC, that implements Particle Gibbs for the stochastic volatility model and a demo repository, SVmodelExamples, containing several R scripts that illustrate the use of this package have been written.
Some of the results of the RcppSMC library extensions, and parts of the example package SVmodelRcppSMC and its demo repository, are illustrated in the next section.
Illustration of some project results
The following illustrations represent two examples of what can now be implemented in the updated library. This is merely a subset of potential use cases, a more detailed summary of library extensions can be found below.
To reproduce the illustrations one has to install the current version of RcppSMC and the package SVmodelRcppSMC from Github and attach the latter:
install.packages("remotes") # can be skipped, if already installed
remotes::install_github("rcppsmc/rcppsmc")
remotes::install_github("ilyaZar/SVmodelRcppSMC")
library(SVmodelRcppSMC)
Project results 1: provide support for tracking ancestral lineages
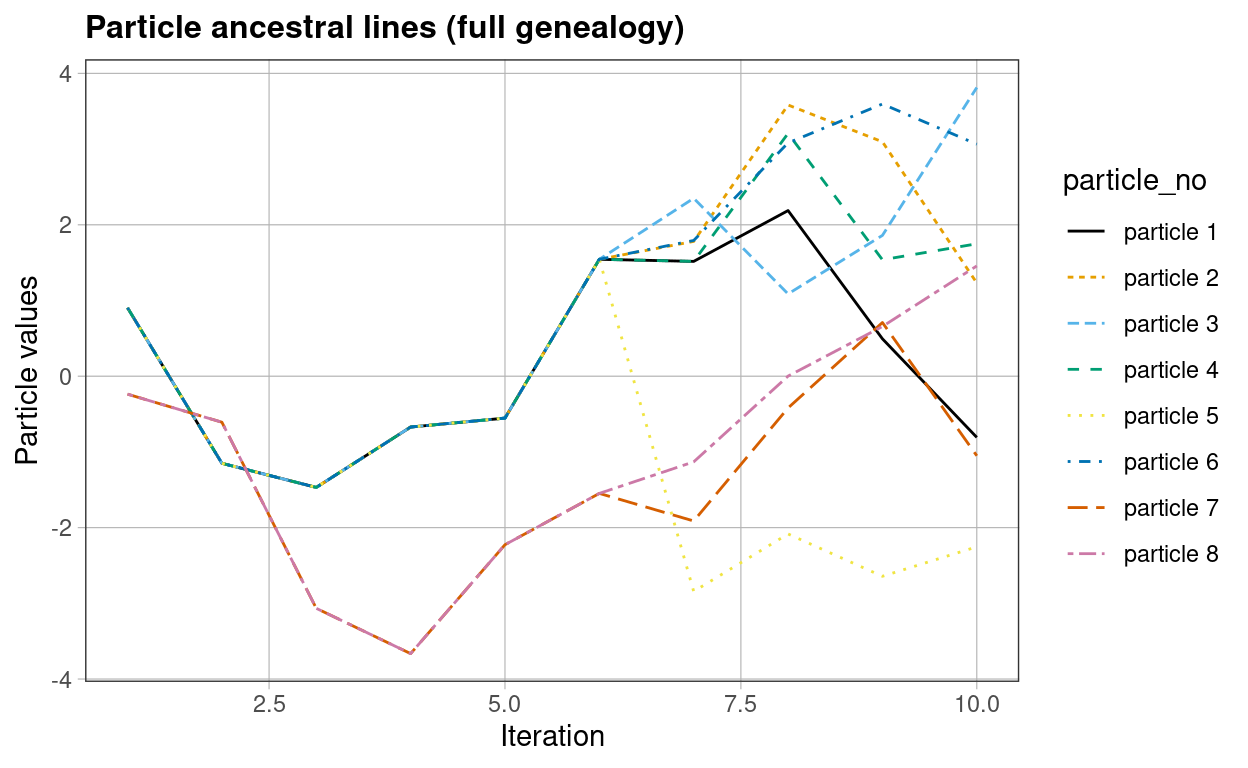
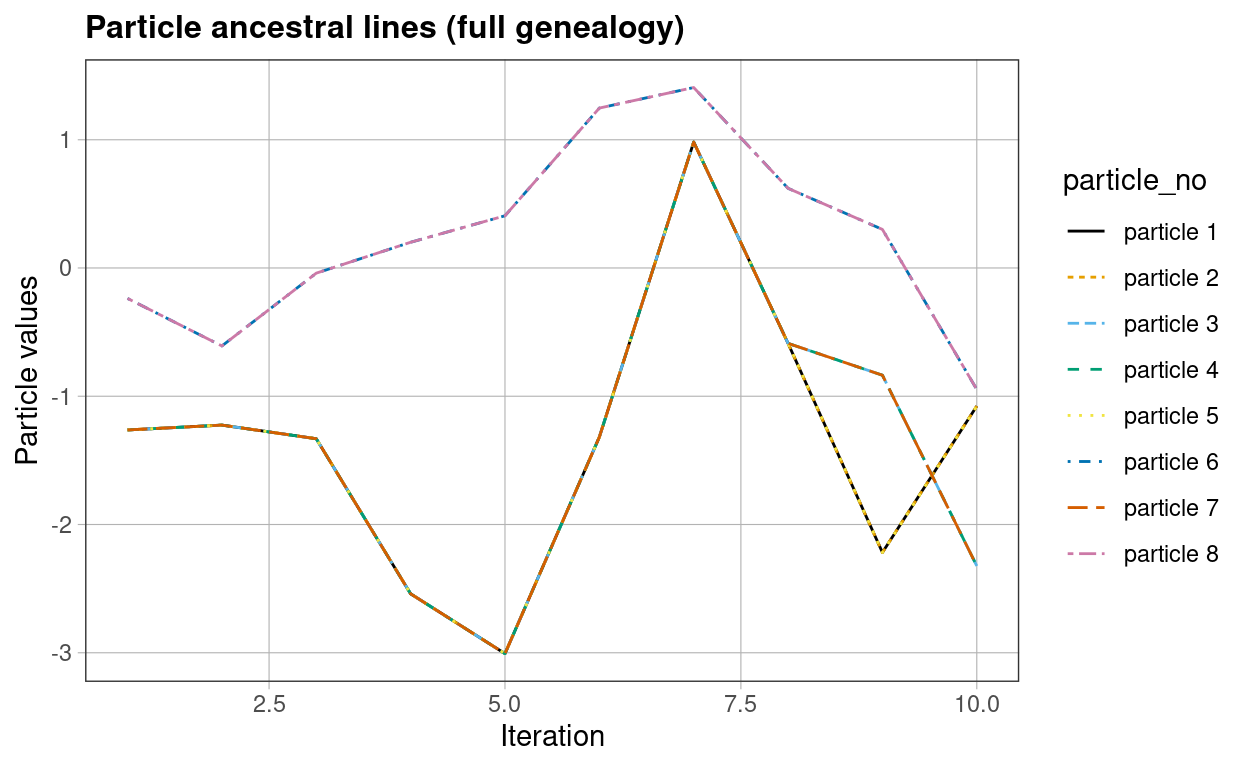
RcppSMC’s underlying C++ code is modified to allow ancestral lineages to be traced. Keeping track of the indices selected in re-sampling allows the genealogy associated with the particles to be traced. Aside from being of independent interest, this information is required to allow advanced hybrid SMC/MCMC algorithms to be implemented.
After installation of SVmodelRcppSMC, run the following script (which is script 09_example.R and be found in the demo repository).
library(SVmodelRcppSMC)
# setting the see for reproducibility
set.seed(123)
# setting model parameters
Tinit <- 10
phiXinit <- 0.9
sigmaXinit <- 0.15
betaYinit <- 0.9
Xinit <- 0
# generate data from SV model
data_simul_sv <- generateDataSimulSV(TT = Tinit,
phiX = phiXinit,
sigmaX = sigmaXinit,
betaY = betaYinit,
initStateX0 = Xinit)
xt <- data_simul_sv$statesXt
yt <- data_simul_sv$measurementsYt
# set small particle number for illustration purposes
particleNumber <- 8
startingVals <- c(phiXinit, 2, 2)
set.seed(42)
# Effective Sample Size small: resampling frequently
# -> weak particle coalescence
res <- svModelALTracking(data = yt,
initVals = startingVals,
particles = particleNumber,
resampleFreq = 0.25)
set.seed(42)
# Effective Sample Size large: resampling less frequently
# -> strong particle coalescence
res <- svModelALTracking(data = yt,
initVals = startingVals,
particles = particleNumber,
resampleFreq = 0.75)
Project results 2: provide support for conditional SMC procedures
The additional template support provided for conditional SMC algorithms is a necessary step towards supporting the implementation of Particle Gibbs, and other advanced SMC/MCMC inferential schemes which make use of them.
To illustrate the new facilities a Particle Gibbs sampler has been implemented and the example code script 03_example.R (which again can be found and be found in the demo repository) can be run (after prior installation of SVmodelRcppSMC, see the previous section).
########################
Iteration: 500 of : 5000 completed.
Current posterior mean: 0.4039 1.9774
########################
Iteration: 1000 of : 5000 completed.
Current posterior mean: 0.3054 1.3476
########################
Iteration: 1500 of : 5000 completed.
Current posterior mean: 0.2694 1.1379
########################
Iteration: 2000 of : 5000 completed.
Current posterior mean: 0.2448 1.0335
########################
Iteration: 2500 of : 5000 completed.
Current posterior mean: 0.2276 0.9711
########################
Iteration: 3000 of : 5000 completed.
Current posterior mean: 0.2179 0.9292
########################
Iteration: 3500 of : 5000 completed.
Current posterior mean: 0.2124 0.8997
########################
Iteration: 4000 of : 5000 completed.
Current posterior mean: 0.2096 0.8774
########################
Iteration: 4500 of : 5000 completed.
Current posterior mean: 0.2062 0.8590
########################
Iteration: 5000 of : 5000 completed.
Current posterior mean: 0.2039 0.8447 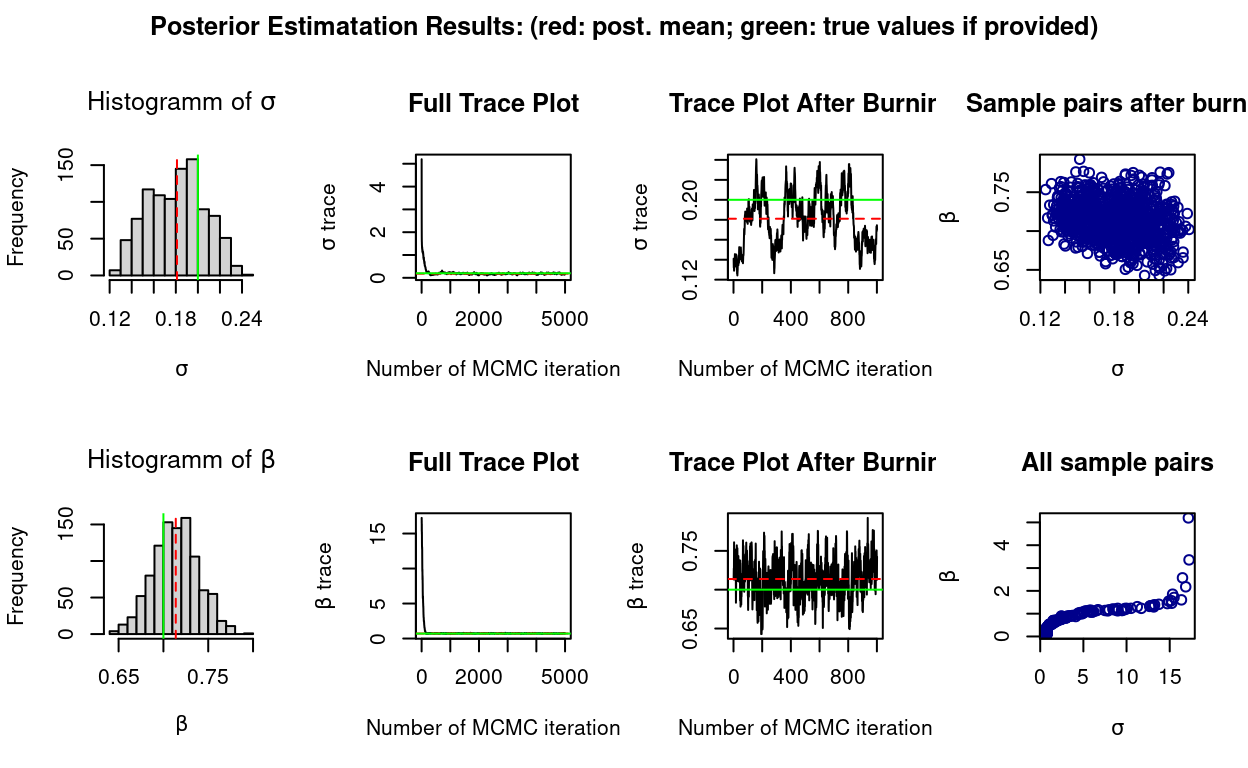
########################
Iteration: 500 of : 5000 completed.
Current posterior mean: 0.3281 1.6102
########################
Iteration: 1000 of : 5000 completed.
Current posterior mean: 0.2465 1.1652
########################
Iteration: 1500 of : 5000 completed.
Current posterior mean: 0.2260 1.0166
########################
Iteration: 2000 of : 5000 completed.
Current posterior mean: 0.2166 0.9423
########################
Iteration: 2500 of : 5000 completed.
Current posterior mean: 0.2096 0.8975
########################
Iteration: 3000 of : 5000 completed.
Current posterior mean: 0.2041 0.8691
########################
Iteration: 3500 of : 5000 completed.
Current posterior mean: 0.1989 0.8485
########################
Iteration: 4000 of : 5000 completed.
Current posterior mean: 0.1951 0.8322
########################
Iteration: 4500 of : 5000 completed.
Current posterior mean: 0.1933 0.8192
########################
Iteration: 5000 of : 5000 completed.
Current posterior mean: 0.1919 0.8094 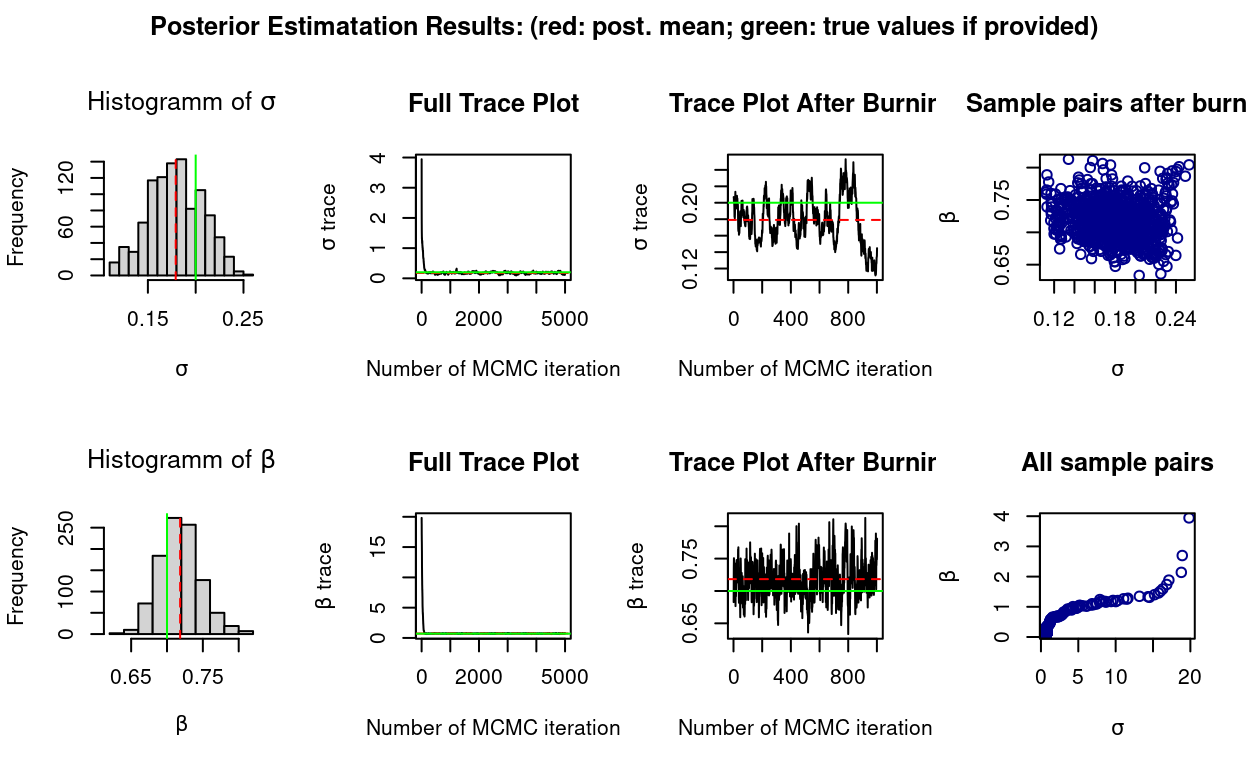
Further details on RcppSMC extensions
The above illustrations represent two examples of what can now be implemented in the updated library. While this is merely a subset of use cases, the detailed extensions are summarized in here.
They relate to template support that allows fine tuning the baseline conditional SMC algorithms by changing the resampling type in a conditional SMC setup. Specifically, either of the following conditional resampling facilities can be used
- multinomial
- stratified
- systematic
- residual
While multinomial resampling is tested well, the other implementations, specifically the conditional residual resampling facility, require some more elaborate testing. Albeit being considerably more challenging (in terms of algorithmic implementation), they have been finalized rather timely to the end of the project time.
Further illustration via use cases one of which being the computation of various Monte Carlo estimates (e.g. the normalizing constant) with its true value within a standard and well studied linear Gaussian setup is probably one fruitful direction for further improvement.
Updated To-Do list and possible future improvements
An updated To-Do list and various ways for future improvements are linked here.